05/05/2021 | Hints from the experts
Mathematical modeling with RS52
Dear users,
We are currently exploring multivariate statistics in order to identify interrelationships. As a part of our project work, we are focusing on customer load data with RS52. This propellent is extremely popular, with well over 100 loads already in the second database. That means we have enough datasets to calibrate our model. We have selected the following variables as inputs for the model:
- Bullet weight
- Charge mass
- Barrel length
- Cartridge length L6 (C.O.L.)
- Barrel cross-section according to CIP values [1]
As our output parameter, we have defined the bullet velocity 5 m from the muzzle (V5). Given our understanding of the physics, the following effects were assumed:
- The greater the bullet weight, the lower the velocity (-)
- The greater the charge mass, the higher the velocity (+)
- The longer the barrel, the higher the velocity (+)
- The longer the cartridge, the greater the volume in the case, the lower the velocity (-)
- The greater the barrel cross-section, the lower the velocity (-)
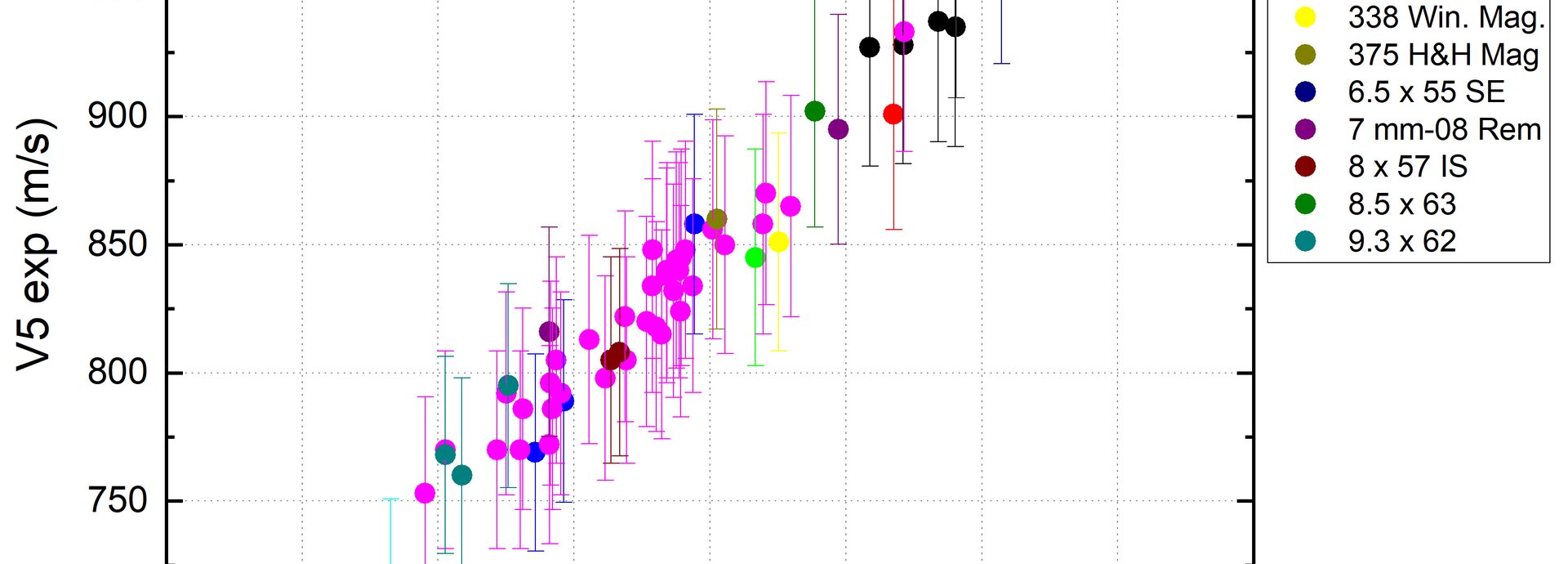
A multiple linear regression with 57 datasets [2] and a correlation coefficient of 0.97 [3] resulted in the following equation for propellent RS52:
V5 = A + a * mc + b * mbu + c * lb + d * lp + e * Q
Variables and values for the coefficients| Variable | Meaning | Unit | Calibration range | Coefficient | Coefficient value |
|---|---|---|---|---|---|
| mc | Powder mass | grains | 26 – 72 | a | 13.53 |
| mbu | Bullet weight | grains | 63 – 250 | b | -1.48 |
| lb | Barrel length | mm | 57 – 91 | c | 0.25 |
| lp | Cartridge length | mm | 420 - 813 | d | -6.37 |
| Q | Area of cross-section | mm2 | 25 – 70 | e | -4.91 |
| A | y-axis section | m/s | - | A | 1011 |
Calculator
This equation now allows us to roughly estimate velocities. The model could be refined further by additionally taking the bullet lengths into account in the dataset. We omitted this refinement because we did not have access to all bullet lengths in sufficient quality. The effective gross case volume could also be considered as a further variable. Anyone wishing to use the simple equation should note that it only calculates the velocity to be expected. The model does not provide any indications of the pressure to be expected. As always, exercise appropriate caution here. The model may only be used for the propellent RS52. We hope that with this model, we have provided you with a further useful tool.
Yours, Carole Bréda and Dominik Antenen
[1] https://bobp.cip-bobp.org/de/tdcc_public
[2] Calculations performed using OriginPro©
[3] When R> 0.95, regression is useful for the physics, according to https://condor.depaul.edu/sjost/it223/documents/correlation.htm